Tomáš Fürst, Ondřej Vencálek, Lucia Houfková
„S čísly si můžete dělat, co chcete!“ říká harpunář Ned Land v jedné slavné verneovce. „Možná v obchodě, ale ve vědě ne!“ oponuje mu profesor Arronax z Pařížského přírodovědeckého muzea.
Pan ředitel ÚZISu Ladislav Dušek nás informoval o tom, že po aplikaci první dávky vakcíny se koronavirem nakazilo 24 377 lidí. To je dle jeho názoru „zanedbatelný podíl na všech nově potvrzených případech“. Redakce Novinek.cz k toto jeho vyjádření obložila z obou stran týmž grafem – aby bylo jasno.
Tak se pojďme podívat, kde narážejí slova pana ředitele na realitu tentokrát. Představme si, že očkování nemá vůbec žádný vliv na to, jestli se nakazíte nebo ne (například očkujeme proti chřipce, ale sledujeme nákazu koronavirem). Přepokládejme, že 10 procent populace je očkováno a řekněme, že zaznamenáme 1000 nových případů infekce. Pokud by očkování bylo úplně neúčinné, můžeme očekávat, že 100 infekcí (deset procent) bude zaznamenáno u očkovaných a zbylých 900 u neočkovaných.
Tuto úvahu jsem provedl pro všechny dny od 1. ledna 2021 do 16. června 2021 (zdroj dat). Obrázek níže ukazuje celkové počty infikovaných každý den (modře) a počty očekávaných infekcí u očkovaných za předpokladu, že vakcinace nemá žádný vliv na to, jestli se nakazíte (červeně). Tedy červený sloupeček je modrý sloupeček násobený podílem populace, která k tomuto dni již měla první dávku vakcíny.
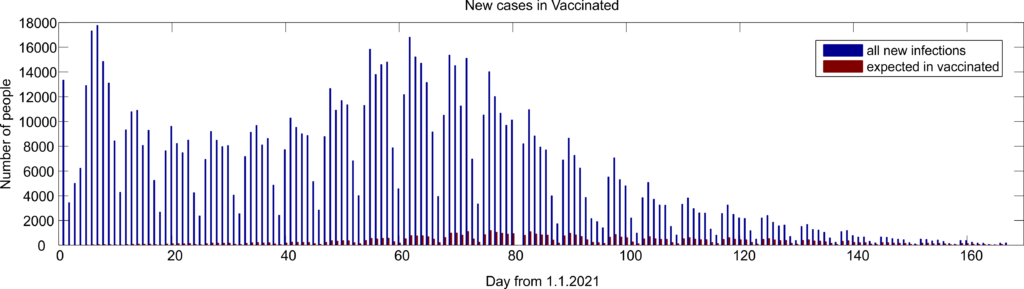
V prvních měsících roku 2021 bylo infekcí hodně, ale očkovaná byla pouze malá část populace. Když potom zlomek očkovaných vyšplhal dost vysoko, počty nakažených byly už poměrně nízké. To způsobí, že součet všech červených sloupečků v grafu je něco přes 57 tisíc.
Za předpokladu, že první dávka vakcíny nemá žádný vliv na to, jestli se nakazíte, bychom 16. června měli očekávat asi 57 tisíc nákaz u očkovaných první dávkou. Ve skutečnosti pozorujeme 24 tisíc těchto nákaz. To není „zcela zanedbatelný podíl“. Tvrzení kolegy Duška je tedy opět hrubě zavádějící a manipulativní. Ačkoliv 24 tisíc je zanedbatelné číslo vzhledem k celkovému počtu nakažených (1.67 milionů od začátku epidemie), rozhodně to není zanedbatelné číslo vzhledem k tomu, kolik takových infekcí by bylo lze očekávat, kdyby vakcinace nefungovala. Vakcinace ale funguje, potřebujeme tedy složitější úvahu.
Označme daný den počet již očkovaných první dávkou V a počet zatím neočkovaných N. Tato dvě čísla jsou každý den známá. Dále označme p pravděpodobnost nákazy v tento konkrétní den. Tohle číslo je každý den jiné a my ho neznáme. Pokud je účinnost vakcíny E, bude tento den celkem M = N*p + V*p*(1-E) nakažených. Protože skutečný počet nakažených M každý den známe, lze z této rovnice vyjádřit p = M / (N + V*(1-E)). Pro každou hodnotu E tak dostaneme odhad čísla p na každý den a z toho spočítáme celkový počet infekcí po první vakcíně a před první vakcínou na konci sledovaného období. A protože tahle čísla od kolegy Duška známe, stačí najít takové E, které vrátí tato dvě čísla nejblíž realitě. V tomto případě vyjde nejblíže realitě E = 60%. První dávka vakcíny tedy snižuje pravděpodobnost nákazy asi na 40 procent její hodnoty u neočkovaných. To jsme věděli už dříve a data z České republiky to jen potvrzují.
ÚZIS tedy ústy svého ředitele pokračuje v tradici matení veřejnosti a manipulace s daty. Možná by stálo za to, aby pan ředitel Dušek věnoval „zanedbatelný podíl“ své mzdy na podporu statistického vzdělávání – pro začátek například 40 procent.
