Tomáš Fürst
Představme si populaci jednoho milionu lidí, kterou budeme sledovat po sto po sobě jdoucích dní. Náhodně vybereme setinu populace, která během sledované doby zemře. Čas úmrtí každého nešťastníka je vybrán náhodně s rovnoměrným rozdělením přes sto sledovaných dnů. Dále náhodně vybereme asi třetinu populace, která si někdy během roku dojde na Hlavní nádraží pro Znamení slunce (to je malý obrázek sluníčka, který je zájemcům nakreslen henou na rameno). Čas udělení Znamení slunce je také náhodně vybrán s rovnoměrným rozdělením přes sto sledovaných dnů. Občas se stane, že čas Znamení bude vylosován až po úmrtí daného člověka – takové znamení prostě ignorujeme.
Máme tedy milion lidí, z nichž asi 10 tisíc postupně zemře a asi 330 tisíc postupně obdrží Znamení slunce. Znamení slunce a úmrtí jsou dle výše uvedeného modelu zcela nezávislé, účinnost Znamení slunce proti úmrtí je přesně nulová. Pro každý den spočteme úmrtnost sluníčkových (tedy procento lidí se Znamením, kteří daný den zemřeli) a úmrtnost nesluníčkových (procento lidí bez Znamení, kteří daný den zemřeli). Není nijak překvapivé, že obě úmrtnosti budou přibližně konstantní, obě budou přibližně stejně velké a rovné přibližně 10-4. Graf ze sta opakování výše popsaného modelu je níže. Je zobrazen sedmidenní centrální klouzavý průměr denní úmrtnosti, abychom mírně potlačili šum.
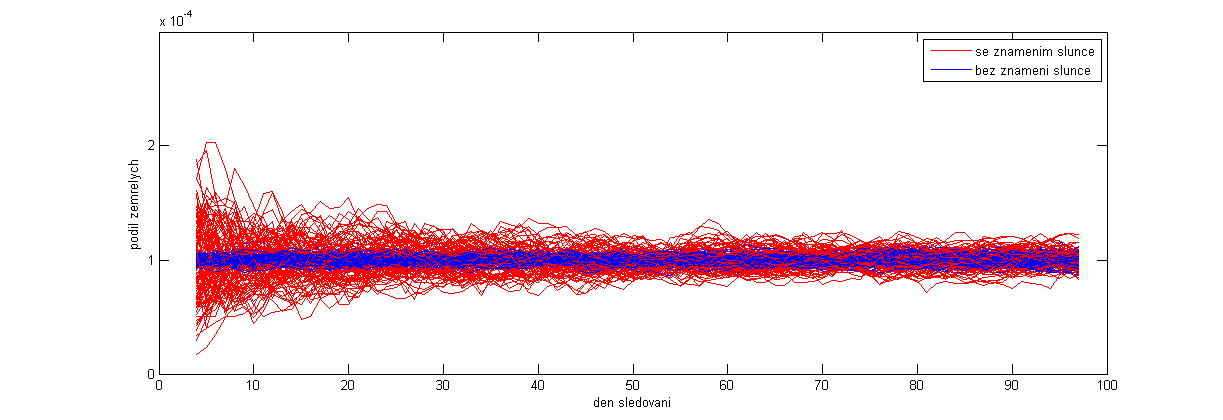
Velký počáteční rozptyl úmrtnosti sluníčkových (červeně) je dán efektem malých čísel – na začátku sledovaného období je lidí se Znamením slunce v populaci ještě velmi málo. Rozptyl úmrtnosti nesluníčkových (modře) naopak velmi zvolna v čase roste, neboť neoznačených v čase ubývá.
Nyní proveďme v modelu drobnou změnu. Každé Znamení slunce, které bylo uděleno méně než 14 dnů před úmrtím, s pravděpodobností p=0.5 zrušme. Tato drobná změna má zachytit fakt, že kdo je na umření, pravděpodobně si nepůjde nechat na Hlavní nádraží kreslit Znamení slunce na rameno. Je třeba upozornit, že z přibližně 330 tisíc udělených Znamení slunce tímto způsobem vyřadíme jen asi šest set, což je zcela zanedbatelné množství. Nyní tedy modelujeme situaci, kdy Znamení slunce s pravděpodobností úmrtí samozřejmě opět nijak nesouvisí (skutečná účinnost je tedy nulová), ovšem dochází k mírnému „selection bias“ v tom smyslu, že lidé, kteří jsou na umření, chodí pro Znamení méně často. Jak bude vypadat výsledek sta běhů tohoto upraveného modelu?
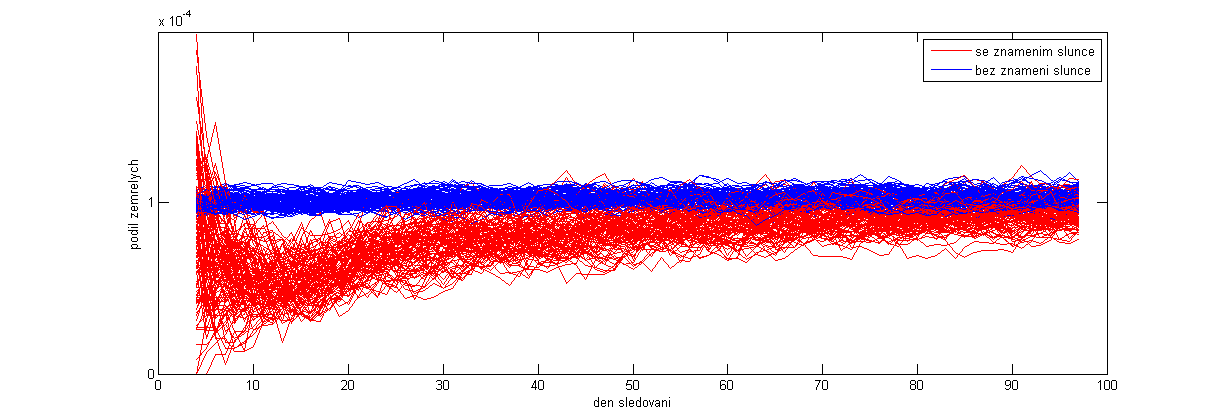
Efekt je překvapivý a dramatický: Znamení slunce má najednou zdánlivě kladnou účinnost proti úmrtí! Tato zdánlivá účinnost z počátečních velmi optimistických hodnot (kolem padesáti procent) postupně v čase klesá až téměř k nule na konci sledovaného období.
Jednoduchou úpravou parametru p jsme schopni dosáhnout jakkoliv vysoké počáteční zdánlivé účinnosti. Znovu připomínám, že oba modely pracují se Znamením slunce, která má nulovou skutečnou účinnost, a druhý model se od prvního liší pouze neudělením asi 0.2% znamení, která v prvním modelu udělena byla.
Už chápete?
